Bir maddenin birim hacminin kütlesine
yoğunluk denir. Yoğunluk saf maddeler için
ayırt edici bir özelliktir. Her saf maddenin belirli bir yoğunluğu vardır Diğer bir değişle birim hacime düşen madde miktarıdır. Yoğunluk kısaca
d ile gösterilir.
Nicelik |
Sembolü |
Ölçüm şekli |
Birimi |
Kütle |
m |
Eşit kollu terazi |
g |
Hacim |
V |
Dereceli silindir |
cm3 |
Yoğunluk |
d |
Hesaplama |
g/cm3 |
Yoğunluğun Hesaplanması
Bir maddenin
kütlesini m,
hacmini V,
yoğunluğunu d ile gösterdiğimizde;
Yoğunluk formülü şu şekilde olur;
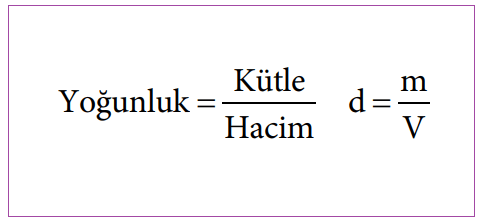
➠
Soru 1: Bir balonun içine 50 cm3 hava konulmuştur ve hava kütlesi 65 gramdır. Havanın yoğunluğunu hesaplayınız.
Çözüm:
Yoğunluk = Kütle / Hacim
Yoğunluk = 65 g / 50 cm3
Yoğunluk = 1,30 g/cm3
➠
Soru 2: 150 cm3'lük bir kavanoza 120 gram su dökülmüştür. Suyun yoğunluğunu hesaplayınız.
Çözüm:
Yoğunluk = Kütle / Hacim
Yoğunluk = 120 g / 150 cm3
Yoğunluk = 0,80 g/cm3
➠
Soru 3: Yoğunluğu 7,87 g/cm3 olan demirden yapılmış bir nesnenin hacmi 200 cm3'tür. Bu nesnenin kütlesini hesaplayınız.
Çözüm:
Kütle = Yoğunluk x Hacim
Kütle = 7,87 g/cm3 x 200 cm3
Kütle = 1574 g
➠
Soru 4: Bir şişeye 250 cm3 sıvı konulmuştur ve sıvının kütlesi 325 gramdır. Sıvının yoğunluğunu hesaplayınız.
Çözüm:
Yoğunluk = Kütle / Hacim
Yoğunluk = 325 g / 250 cm3
Yoğunluk = 1,30 g/cm3
➠
Soru 5: Ali'nin coğrafya kitabının kütlesi 600 gram, yoğunluğu 0,80 g/cm3 olduğuna göre Ali'nin kitabının hacmini hesaplayınız.
Çözüm:
Hacim = Kütle / Yoğunluk
Hacim = 600 g / 0,80 g/cm3
Hacim = 750 cm3
Madde |
Yoğunluk (g/cm³) |
Madde |
Yoğunluk (g/cm³) |
Altın |
19,30 |
Gliserin |
1,26 |
Demir |
7,8 |
Grafit |
2,10 |
Kurşun |
11,30 |
Elmas |
3,50 |
Bakır |
8,90 |
Cam |
2,60 |
Su |
1,00 |
Porselen |
2,25 |
Buz |
0,90 |
Tahta |
0,5 |
Zeytinyağı |
0,92 |
Çelik |
7,85 |
Etil alkol |
0,81 |
Alçı |
2,32 |
Benzen |
0,89 |
Kâğıt |
0,95 |
Alüminyum |
2,70 |
|
|
Düzgün Şekli Olmayan Katıların Yoğunluğunu Hesaplama
Düzgün şekli olmayan katıların yoğunluğu, çeşitli sebeplerle ölçmek isteyebileceğimiz bir özelliktir. Bu tür katıların yoğunluğunu belirlemek için kullanılabilecek birkaç yöntem vardır. Bu makalede, düzgün şekli olmayan katıların yoğunluğunu belirlemek için kullanılan yöntemlerden ve örneklerden bahsedeceğiz.
Batma-Çıkma Yöntemi (Arşimet Prensibi)
Bu yöntemde, öncelikle katının kütlesi ölçülür. Ardından, katı bir sıvıya daldırılır ve sıvının seviyesindeki değişiklik ölçülür. Bu değişiklik, katının yer değiştirdiği sıvı hacmini verir. Arşimet prensibine göre, katıya etki eden itici kuvvet, yer değiştiren sıvının kütlesiyle eşittir. Bu bilgiler kullanılarak katının yoğunluğu hesaplanabilir.
Örnek:
Düzgün şekli olmayan bir taşın kütlesini ölçtüğümüzde 300 g olduğunu belirleyelim. Taşı bir ölçüm kabındaki suya daldırarak, su seviyesindeki yükselmeyi ölçtüğümüzde 100 cm³ olduğunu bulalım.
Yoğunluk = Kütle / Hacim
Yoğunluk = 300 g / 100 cm³
Yoğunluk = 3 g/cm³
Düzgün şekli olmayan katıların yoğunluğunu ölçmek, malzeme bilimi, inşaat, kimya ve diğer birçok alanda önemli uygulamalara sahiptir. Örneğin, maden endüstrisinde, cevherlerin yoğunluğunu belirlemek için bu yöntemler kullanılabilir. Ayrıca, arkeologlar, antik nesnelerin malzemelerini ve yapım yöntemlerini incelemek için bu yöntemleri kullanabilirler.
Soru 1: İçerisinde 50 cm³ su bulunan bir beherin kütlesi 100 g olarak ölçülmüştür. Beherin içine bir metal parçası atıldıktan sonra kütlesi 220 g, su seviyesi 70 cm³ ölçülmüştür. Su beherden taşmadığına göre metal parçasının yoğunluğunu bulunuz.
Çözüm:
İlk olarak metal parçasının kütlesini bulalım:
Metal kütle = Son kütle - İlk kütle = 220 g - 100 g = 120 g
Metal parçasının hacmini bulalım:
Hacim değişimi = Son su seviyesi - İlk su seviyesi = 70 cm³ - 50 cm³ = 20 cm³
Metal parçasının yoğunluğunu hesaplayalım:
Yoğunluk = Kütle / Hacim = 120 g / 20 cm³ = 6 g/cm³
Soru 2: İçerisinde 40 cm³ su bulunan bir ölçüm kabının kütlesi 80 g olarak ölçülmüştür. Ölçüm kabının içine bir plastik parçası atıldıktan sonra kütlesi 95 g, su seviyesi 45 cm³ ölçülmüştür. Su ölçüm kabından taşmadığına göre plastik parçasının yoğunluğunu bulunuz.
Çözüm:
İlk olarak plastik parçasının kütlesini bulalım:
Plastik kütle = Son kütle - İlk kütle = 95 g - 80 g = 15 g
Plastik parçasının hacmini bulalım:
Hacim değişimi = Son su seviyesi - İlk su seviyesi = 45 cm³ - 40 cm³ = 5 cm³
Plastik parçasının yoğunluğunu hesaplayalım:
Yoğunluk = Kütle / Hacim = 15 g / 5 cm³ = 3 g/cm³
Soru 3: İçerisinde 75 cm³ su bulunan bir kaba kütlesi 150 g olarak ölçülmüştür. Kabın içine bir seramik parçası atıldıktan sonra kütlesi 200 g, su seviyesi 95 cm³ ölçülmüştür. Su kaptan taşmadığına göre seramik parçasının yoğunluğunu bulunuz.
Çözüm:
İlk olarak seramik parçasının kütlesini bulalım:
Seramik kütle = Son kütle - İlk kütle = 200 g - 150 g = 50 g
Seramik parçasının hacmini bulalım:
Hacim değişimi = Son su seviyesi - İlk su seviyesi = 95 cm³ - 75 cm³ = 20 cm³
Seramik parçasının yoğunluğunu hesaplayalım:
Yoğunluk = Kütle / Hacim = 50 g / 20 cm³ = 2,5 g/cm³
Soru 4: İçerisinde 80 cm³ su bulunan bir ölçüm kabının kütlesi 160 g olarak ölçülmüştür. Ölçüm kabının içine bir kum parçası atıldıktan sonra kütlesi 210 g, su seviyesi 105 cm³ ölçülmüştür. Su ölçüm kabından taşmadığına göre kum parçasının yoğunluğunu bulunuz.
Çözüm:
İlk olarak kum parçasının kütlesini bulalım:
Kum kütle = Son kütle - İlk kütle = 210 g - 160 g = 50 g
Kum parçasının hacmini bulalım:
Hacim değişimi = Son su seviyesi - İlk su seviyesi = 105 cm³ - 80 cm³ = 25 cm³
Kum parçasının yoğunluğunu hesaplayalım:
Yoğunluk = Kütle / Hacim = 50 g / 25 cm³ = 2 g/cm³
Soru 5: İçerisinde 100 cm³ su bulunan bir piknometrenin kütlesi 200 g olarak ölçülmüştür. Piknometrenin içine bir tahta parçası atıldıktan sonra kütlesi 225 g, su seviyesi 110 cm³ ölçülmüştür. Su piknometreden taşmadığına göre tahta parçasının yoğunluğunu bulunuz.
Çözüm:
İlk olarak tahta parçasının kütlesini bulalım:
Tahta kütle = Son kütle - İlk kütle = 225 g - 200 g = 25 g
Tahta parçasının hacmini bulalım:
Hacim değişimi = Son su seviyesi - İlk su seviyesi = 110 cm³ - 100 cm³ = 10 cm³
Tahta parçasının yoğunluğunu hesaplayalım:
Yoğunluk = Kütle / Hacim = 25 g / 10 cm³ = 2,5 g/cm³
Bu sorular ve çözümleri, düzgün şekli olmayan katıların yoğunluğunu belirlemek için kullanılan yöntemleri ve hesaplamaları göstermektedir. Bu yöntemler, farklı katıların yoğunluklarını belirlemekte etkili olup, çeşitli uygulamalara sahiptir.
Sıvıların Yoğunluğunu Hesaplama
Sıvı yoğunluğu, bir sıvının belirli bir hacmindeki kütleyi ifade eder ve genellikle gram/cm³ cinsinden ölçülür.
Sıvıların yoğunluğunu hesaplamak için, öncelikle sıvının kütlesi ve hacmi ölçülür. Bu ölçümler yoğunluğun hesaplanması için kullanılır.
Yoğunluk = Kütle / Hacim
Örnek:
100 cm³'lük bir beherin içindeki suyun kütlesi 100 g olarak ölçülmüştür. Su yoğunluğunu hesaplayalım.
Yoğunluk = Kütle / Hacim
Yoğunluk = 100 g / 100 cm³
Yoğunluk = 1 g/cm³
Suyun yoğunluğunun canlılar için önemi
Suyun yoğunluğunun canlılar için önemi, birkaç temel sebep ve etkiye dayanmaktadır. Suyun yoğunluğu ve sıcaklıkla olan ilişkisi, suyun hareketi, canlıların yaşam ortamı ve biyolojik süreçleri üzerinde önemli bir rol oynar.
Su, 4°C'de en yüksek yoğunluğa (1 g/cm³) ulaşır ve bu sıcaklıkta yoğunluk değeri anormaldir. Bu özellik, suyun soğuduğunda yoğunluğunun artması ve donduğunda yoğunluğunun azalmasıyla sonuçlanır. Buz, sıvı suya göre daha az yoğun olduğu için yüzeye çıkar ve yüzeyde kalır. Bu durum, sucul canlılar için yaşamsal öneme sahiptir çünkü su yüzeyindeki buz tabakası, altındaki sıvı suyun donmasını engelleyerek sucul canlıların yaşamını sürdürebilmesine olanak sağlar.
Suyun yoğunluğu, sıcaklıkla olan ilişkisi nedeniyle, su kütlelerinde dikey ve yatay hareketler meydana gelir. Bu hareketler, denizlerde ve okyanuslarda ısı ve enerji transferine yol açar. Sıcak su, soğuk suya göre daha az yoğundur ve yüzeye yükselir, soğuk su ise daha yoğun olduğu için alçalır. Bu süreç, sucul ekosistemlerde oksijen ve besin döngüsünü etkiler ve sucul canlıların yaşaması için uygun ortamlar sağlar.
Su, 4°C'de en yüksek yoğunluğa ulaşır ve bu özellik, suyun soğuyarak donduğunda hacminin artmasıyla sonuçlanır. Bu durum, sucul canlılar için yaşamsal öneme sahiptir.
Buzun yüzdüğü: Su donduğunda yoğunluğu azaldığı için buz, sıvı suya göre daha az yoğundur ve yüzeye çıkar. Bu durum, sucul ekosistemlerin korunmasına ve sucul canlıların yaşamını sürdürebilmesine olanak sağlar.
Suyun yoğunluğu ve sıcaklıkla olan ilişkisi, su kütlelerinde dikey ve yatay hareketlere yol açar. Bu hareketler, denizlerde ve okyanuslarda ısı ve enerji transferini sağlar.
Suyun yoğunluğu ve polar yapısı, hücre içinde gerçekleşen biyokimyasal reaksiyonların etkili bir şekilde sürdürülmesine yardımcı olur.
Suyun yoğunluğu, sucul canlılar üzerindeki hidrostatik basıncı etkiler. Bu basınç, canlıların derinliklere göre yaşam ve adaptasyon stratejilerini belirler.
Katı, Sıvı ve Gaz Maddelerin Yoğunlukları
Katı ve sıvı maddeler genellikle ısıtıldığında genleşir ve soğutulduğunda büzüşür; bu durum yoğunluklarında değişikliklere yol açar. Ancak, su bu kuralın istisnasıdır. Su soğutulduğunda ve donduğunda hacmi artar ve yoğunluğu azalır. Aynı şekilde, ısıtıldığında ve buharlaştığında da hacmi artar. Suyun bu özel özelliği, canlılar için büyük öneme sahiptir.
Katı maddeler ısıtıldığında genleşir, soğutulduğunda büzüşür: Isıtma, tanecikler arasındaki uzaklığın artmasına ve hacmin büyümesine yol açar. Soğutma, taneciklerin birbirine yaklaşması ve hacmin küçülmesiyle sonuçlanır.
Sıvı maddelerin yoğunluğu ısıya bağlı olarak değişir: Sıvılar soğutulduğunda tanecikler yavaşlar, birbirine yaklaşır ve yoğunluk artar. Isıtıldığında ise tanecikler hızlanır, birbirinden uzaklaşır ve yoğunluk azalır.
Su, diğer sıvılardan farklıdır: Su soğutulduğunda ve donduğunda, aynı zamanda ısıtıldığında ve buharlaştığında da hacmi artar, yoğunluğu azalır.
Buz dağlarının suyun üzerinde yüzmesi, suyun hangi özelliği ile açıklanabilir?
Buz dağlarının suyun üzerinde yüzmesi, suyun "kaldırma kuvveti" veya "yüksek yoğunluk" özelliği ile açıklanabilir. Buz, suyun katı hali olan buzun yoğunluğu, suyun yoğunluğundan daha düşüktür. Bu nedenle, buz parçaları suyun üzerinde kalmakta ve yüzmektedir. Bu özellik, Archimedes prensibi ile de bağlantılıdır, yani su, batan bir cisim üzerine, kendi ağırlığına eşit bir kaldırma kuvveti uygular.
Buzun yoğunluğu suyun yoğunluğundan düşük olduğu için, su buzun üzerinde bir kaldırma kuvveti uygular ve buz yüzeye çıkar.
